Mevcut verilerden hareket ederek geleceğin tahmin edilmesinde faydalanılan ve veri madenciliği teknikleri içerisinde en yaygın kullanıma sahip olan sınıflama ve regresyon modelleri arasındaki temel fark, tahmin edilen bağımlı değişkenin kategorik veya süreklilik gösteren bir değere sahip olmasıdır [1]. Sınıflamada tahmin edilen bağımlı değişken kategorik, Regresyonda ise süreklilik gösteren bir değere sahiptir.
Örneğin, bir sınıflama modeli banka kredi uygulamalarının güvenli veya riskli olmalarını kategorize etmek amacıyla kurulurken, regresyon modeli geliri ve mesleği verilen potansiyel müşterilerin bilgisayar ürünleri alırken yapacakları harcamaları tahmin etmek için kurulabilir. Ancak çok terimli lojistik regresyon (multinomial logistic regression) gibi kategorik değerlerin de tahmin edilmesine imkan sağlayan tekniklerle, her iki model giderek birbirine yaklaşmakta ve bunun bir sonucu olarak aynı tekniklerden yararlanılması mümkün olmaktadır [1].
Sınıflama, verinin önceden belirlenen çıktılara uygun olarak ayrıştırılmasını sağlayan bir tekniktir. Çıktılar, önceden bilindiği için sınıflama, veri kümesini denetimli (supervised) olarak öğrenir [2].
Örneğin, A finans hizmetleri şirketi müşterilerinin yeni bir yatırım fırsatıyla ilgilenip ilgilenmediğini öğrenmek istemektedir. Daha önceden benzer bir ürün satmıştır ve geçmiş veriler hangi müşterilerin önceki teklife cevap verdiğini göstermektedir. Amaç; bu teklife cevap veren müşterilerin özelliklerini belirlemek ve böylece pazarlama ve satış çalışmalarını daha etkin yürütmektir. Müşteri kayıtlarında müşterinin önceki teklife cevap verip vermediğini gösteren “evet”/ “hayır” şeklinde bir alan bulunur. Bu alan “hedef” ya da “bağımlı” değişken (target variable) olarak adlandırılır. Amaç, müşterilerin diğer niteliklerinin (gelir düzeyi, iş türü, yaş, medeni durum, kaç yıldır müşteri olduğu, satın aldığı diğer ürün ve yatırım türleri) hedef değişken üzerindeki etkilerini analiz etmektir. Analizde yer alan diğer nitelikler “bağımsız” ya da “ tahminci” değişken adını alır [3].
Sınıflandırma ve regresyon modellerinde kullanılan başlıca teknikler şunlardır [3]:
- Karar Ağaçları (Decision Trees),
- Yapay Sinir Ağları (Artificial Neural Networks),
- Genetik Algoritmalar (Genetic Algorithms),
- K-En Yakın Komşu (K-Nearest Neighbour),
- Regresyon Analizi ,
- Naive-Bayes ,
- Kaba Kümeler.
Karar ağaçları
Kuruluşlarının ucuz olması, yorumlanmalarının kolay olması, veri tabanı sistemleri ile kolayca entegre edilebilmeleri ve güvenilirliklerinin iyi olması sebepleri ile en yaygın kullanıma sahip veri madenciliği sınıflama modeli tekniği karar ağaçlarıdır. Karar ağacı, adından da anlaşılacağı gibi bir ağaç görünümünde, tahmin edici bir tekniktir. Karar ağaçları düğümler ve dallardan oluşan anlaşılması kolay bir tekniktir. Karar ağacında bulunan her bir dalın belirli bir olasılığı mevcuttur. Bu sayede son dallardan köke veya istediğimiz yere ulaşana kadar olasılıkları hesaplamak mümkündür.
SQL sorgusuna kolay dönüştürülebilir yapısıyla en popüler segmentasyon yöntemlerinden birisidir. En yaygın kullanılan karar ağacı yöntemleri şunlardır [4]:
- CHAID (Chi-Squared Automatic Interaction Detector , Kass 1980),
- C&RT (Classification and Regression Trees, Breiman ve Friedman, 1984),
- ID3 (Induction of Decision Trees, Quinlan, 1986),
- C4.5 (Quinlan, 1993),
- C5.0.
Yapay sinir ağları
Yapay sinir ağları (YSA), temelde tamamen insan beyni örneklenerek geliştirilmiş bir teknolojidir. Öğrenme, hatırlama, düşünme gibi tüm insan davranışlarının temelinde sinir hücreleri bulunmaktadır. İnsan beyninde tahminen 10 üzeri 11 adet sinir hücresi olduğu düşünülmektedir. Bu sinir hücreleri arasında sonsuz denilebilecek sayıda sinaptik birleşme denilen sinirler arası bağ vardır. İnsan beyninin öğrenme yoluyla yeni bilgiler üretebilme, keşfedebilme, düşünme ve gözlemlemeye yönelik yeteneklerini, yardım almadan yapabilen sistemler geliştirmek için tasarlanmışlardır. YSA’nın hesaplama ve bilgi işleme gücünü, paralel dağılmış yapısından, öğrenebilme ve genelleme yeteneğinden aldığı söylenebilir. Genelleme, eğitim ya da öğrenme sürecinde karşılaşılmayan girişler için de YSA’nın uygun tepkileri üretmesi olarak tanımlanır. Bu üstün özellikleri, YSA’nın karmaşık problemleri çözebilme yeteneğini gösterir [5].
Bu yöntem, belirli bir profile uyuşması için kalıp düzenlerini kontrol etmekte ve bu süreç içerisinde belli bir öğrenme faaliyeti gerçekleştirerek sistemi geliştirmektedir. Yapay sinir ağlarında kullanılan öğrenme algoritmaları, veriden üniteler arasındaki bağlantı ağırlıklarını hesaplar. Yapay sinir ağları istatistiksel yöntemler gibi veri hakkında parametrik bir model varsaymaz. Yani uygulama alanı daha geniştir ve bellek tabanlı yöntemler kadar yüksek işlem ve bellek gerektirmez [6]. Bir yapay sinir ağı belirli bir amaç için oluşturulur ve insanlar gibi örnekler sayesinde öğrenir. Yapay sinir ağları tekrarlanan girdiler sayesinde kendi yapısını, ağırlığını değiştirir ve aynen canlıların sinir sistemi gibi adapte olabilen bir yapıya sahiptir. Yapay sinir ağları, öğrenmenin yanı sıra bilgiler arasında ilişkiler oluşturma yeteneğine de sahiptir.
Yapay sinir ağlarının temel işlevleri şu şekilde belirtilebilir [7]:
- Öngörü (Prediction) veya tahminleme: İleriki satışlar, hava tahminleri, at yarışları, çevresel risk, …
- Sınıflandırma (Classification) ve Kümeleme (Clustering): Müşteri profilleri, tıbbi teşhis, ses ve şekil tanıma, hücre tipleri …
- Kontrol (Control): Erken uyarı için uçaklarda ses ve titreşim düzeyleri, …
Ayrıca, Veri Birleştirme (Data Association), Kavramsallaştırma (Data Conceptualization) ve Filtreleme (Data Filtering) için de kullanılabilir.
Yapay sinir ağlarının endüstriyel uygulamalar, finans uygulamaları, askeri ve savunma uygulamaları, tıp ve sağlık uygulamaları, mühendislik uygulamaları, robotbilim, görüntü işleme, örüntü tanıma dışında iletişim sanayi, eğlence amaçlı tahmin gibi özel uygulama alanları da bulunmaktadır [7].
Bir yapay sinir ağı hücresi temel olarak girdilerden, ağırlıklardan, toplama işlevinden ve çıktıdan oluşur.
 |
| Yapay sinir hücresi [8] |
Yapay sinir ağları (YSA), insan beyninden esinlenerek geliştirilmiştir. Değişen ağırlıklarda bağlantılarla birbirine bağlanan ve her biri kendi belleğine sahip işlem elemanlarından oluşan bilgi işleme yapılarıdır. Yukarıda görüldüğü gibi YSA, kendisine verilen girdiye ağırlıklar ve aktivasyon fonksiyonunu kullanarak bir çıktı üretmektedir [8].
Genelde, verilen bir girdi kümesine karşılık çıktı değerleri verilerek belirtilen öğrenme kuralına göre ağırlık değerleri otomatik olarak değiştirilmektedir. Eğitim verisinin tamamlanmasından sonra eğitilmiş olan ağ, ağırlık değerlerinin son durumuna göre, verilen herhangi bir veri kümesinin sonucunu tahminleyebilmektedir. Yapay sinir ağı bir dizi sinir hücresinin ileri sürümlü ve geri beslemeli bağlantı şekilleri ile birbirine bağlanması ile oluşur. Günümüzde, belirli amaçlarla ve değişik alanlarda kullanılmaya uygun birçok yapay sinir ağı modeli (Perceptron, Adaline, MLP, LVQ, Hopfield, Recurrent, SOM, ART ve PCA gibi) geliştirilmiştir. Öğrenme çeşitlerinden gözetimli öğrenme, gözetimsiz öğrenme, takviyeli öğrenme ve yarı gözetimli stratejiler kullanılmaktadır [7].
Genetik algoritmalar
Algoritma ilk olarak popülasyon adı verilen bir çözüm kümesi (öğrenme veri kümesi) ile başlatılır. Bir popülasyondan alınan sonuçlar bir öncekinden daha iyi olacağı beklenen yeni bir popülasyon oluşturmak için kullanılır. Evrim süreci tamamlandığında bağımlılık kuralları veya sınıf modelleri ortaya konmuş olur [9].
Yapay sinir ağları gibi biyolojik sistemlerden esinlenerek tasarlanmış bir tür makine öğrenimi sistemidir. Evrim teorisini modelleyen bu algoritmalar, doğal şartlara en fazla uyum sağlayan bireyin hayatta kalabilmesi temeline dayanan doğal seleksiyonu bilgisayar ortamında simüle eder [10].
Genetik algoritmalar, optimizasyon problemlerinde olduğu gibi sınıflandırma için de kullanılabilir. Veri madenciliğinde, diğer algoritmaların uygunluğunu değerlendirmek için kullanılabilirler [11].
Problemlere tek bir çözüm üretmek yerine farklı çözümlerden oluşan bir çözüm kümesi üreten genetik algoritma sayesinde, arama uzayında aynı anda birçok nokta değerlendirilmekte ve sonuçta bütünsel çözüme ulaşma olasılığı yükselmektedir. Çözüm kümesindeki çözümler birbirinden tamamen bağımsızdır. Her biri çok boyutlu uzay üzerinde bir vektördür. Problem için olası pek çok çözümü temsil eden kümeler genetik algoritma terminolojisinde nüfus adını alır. Nüfuslar vektör veya birey adı verilen sayı dizilerinden oluşur. Birey içindeki her bir elemana gen adı verilir. Nüfustaki bireyler evrimsel süreç içinde genetik algoritma işlemcileri tarafından belirlenir [5].
K-En yakın komşu
Veri madenciliğinde sınıflama amacıyla kullanılan bir diğer teknik ise örnekseme yoluyla öğrenmeye dayanan k-en yakın komşu algoritmasıdır. Bu teknikte tüm örneklemler bir örüntü uzayında saklanır. Algoritma, bilinmeyen bir örneklemin hangi sınıfa dahil olduğunu belirlemek için örüntü uzayını araştırarak bilinmeyen örnekleme en yakın olan k örneklemi bulur. Yakınlık Öklid uzaklığı ile tanımlanır. Daha sonra bilinmeyen örneklem, k en yakın komşu içinden en çok benzediği sınıfa atanır. K-en yakın komşu algoritması, aynı zamanda bilinmeyen örneklem için bir gerçek değerin tahmininde de kullanılabilir.
Bu yöntemin tercih edilme sebebi, sayısı bilinen veri kümeleri için hızlı ve verimli olmasıdır [12]. Özellikle büyük veri tabanlarında kullanılan bir sınıflandırma tekniğidir. Sınıflandırılmak istenen nesnenin ait olduğu kümeyi, en yakınında yer alan K birim nesneden en fazla birime ait olanla aynı kümede sınıflandırması mantığına dayanmaktadır [13].
Bu yöntemde eğitim örnekleri n-boyutlu sayısal niteliklerle tanımlanır. Her örnek n-boyutlu uzayda bir noktayı gösterir. Bu yolla, bütün eğitim örnekleri n-boyutlu örnek uzayda depolanır. Bu k-eğitim örnekleri bilinmeyen örneğe k en yakın komşudur. Öklid uzaklığı X=(x1,x2,….,xn) ve Y=(y1,y2,…….,yn) arasındadır. Bilinmeyen örnek k-komşularının arasında en sık olan sınıfa verilir. k=1 olduğunda, bilinmeyen örnek uzayında en yakın eğitim örneğinin sınıfıdır. En yakın komşu sınıflandırıcısı örnek-tabanlı ya da tembel-öğrenenlerdir (lazylearners); bunlar bütün eğitim örneklerini depolarlar ve yeni bir örnek sınıflandırmaya gerek olmadıkça bir sınıflandırıcı yapılandırmazlar. Tembel-öğrenenler, potansiyel komşularının sayısı etiketlenmemiş örneklerin sayısına göre büyükse hesaplama maliyetini arttırabilir. Bu nedenle etkili indeksleme teknikleri gerektirir. Beklendiği gibi lazy-learning yöntemleri eager yöntemlerden daha hızlıdır fakat bütün hesaplamalar geciktirildiğinde sınıflanma yavaşlar. En yakın komşu sınıflandırıcısı kestirim içinde kullanılabilir [11].
Sınıflandırma problemini çözen denetimli öğrenme yöntemleri arasında yer alır. Yöntemde sınıflandırma yapılacak verilerin öğrenme kümesindeki normal davranış verilerine benzerlikleri hesaplanarak, en yakın olduğu düşünülen k verinin ortalamasıyla, belirlenen eşik değere göre sınıflara atamaları yapılır. Önemli olan, her bir sınıfın özelliklerinin önceden net bir şekilde belirlenmiş olmasıdır. Yöntemin performansını k en yakın komşu sayısı, eşik değer, benzerlik ölçümü ve öğrenme kümesindeki normal davranışların yeterli sayıda olması kriterleri etkilemektedir [14].
Regresyon analizi
Regresyon analizi, bir ya da daha fazla bağımsız değişken ile hedef değişken arasındaki ilişkiyi matematiksel olarak modelleyen bir yöntemdir. Veri madenciliğinde yaygın olarak kullanılan regresyon modellerinden doğrusal regresyonda tahmin edilecek olan hedef değişken sürekli değer alırken, lojistik regresyonda hedef değişken kesikli bir değer almaktadır. Doğrusal regresyonda hedef değişkenin değeri, lojistik regresyonda ise hedef değişkenin alabileceği değerlerden birinin gerçekleşme olasılığı tahmin edilmektedir [15].
Doğrusal, doğrusal olmayan ve lojistik modelleme alternatifleri imkanı vardır. Bağımsız değişken olarak anılan tahmin edici değişkenlerin, bağımlı değişken denilen tahmin edilecek değişken değerini belirleyecek ağırlıklandırmaları içerecek bir bağımsız değişkenler birleşimidir [4].
Naive-Bayes
Naive Bayes algoritması her kriterin sonuca olan etkilerinin olasılık olarak hesaplanması temeline dayanmaktadır. Örneğin, sağlık sektöründe bir kişinin tahlil sonuçlarının değerlendirilerek bir hastalığa yakalanmış olup olmama olasılığının değerlendirilmesinde de sıkça kullanılmaktadır.
Naive Bayes, hedef değişkenle bağımsız değişkenler arasındaki ilişkiyi analiz eden tahminci ve tanımlayıcı bir sınıflama algoritmasıdır. Sürekli veri ile çalışmaz. Bu sebeple sürekli değerleri içeren bağımlı ya da bağımsız değişkenler kategorik hale getirilmelidir. Örneğin; bağımsız değişkenlerden biri yaş ise, sürekli değerler “<20” “21–30”, “31–40” gibi yaş aralıklarına dönüştürülmelidir. Naive Bayes modelin öğrenilmesi esnasında, her çıktının öğrenme kümesinde kaç kere meydana geldiğini hesaplar. Bulunan bu değer öncelikli olasılık olarak adlandırılır. Örneğin, bir banka kredi kartı başvurularını “iyi” ve “kötü” risk sınıflarında gruplandırmak istemektedir. İyi risk çıktısı toplam 5 vaka içinde 2 kere meydana geldiyse iyi risk için öncelikli olasılık 0,4'tür. Bu durum, “Kredi kartı için başvuran biri hakkında hiçbir şey bilinmiyorsa, bu kişi 0,4 olasılıkla iyi risk grubundadır.” olarak yorumlanır. Naive Bayes aynı zamanda her bağımsız değişken / bağımlı değişken kombinasyonunun meydana gelme sıklığını bulur. Bu sıklıklar öncelikli olasılıklarla birleştirilmek suretiyle tahminde kullanılır [3].
Kaba kümeler
Kaba küme teorisi 1970‟li yıllarda Pawlak tarafından geliştirilmiştir. Kaba küme teorisinde bir yaklaştırma uzayı ve bir kümenin alt ve üst yaklaştırmaları vardır. Yaklaştırma uzayı, ilgilenilen alanı ayrı kategorilerde sınıflandırır. Alt yakınlaştırma belirli bir alt kümeye ait olduğu kesin olarak bilinen nesnelerin tanımıdır. Üst yakınlaştırma ise alt kümeye ait olması olası nesnelerin tanımıdır. Alt ve üst sınırlar arasında tanımlanan herhangi bir nesne ise “kaba küme” olarak adlandırılır [16].
Kümeleme
Nesneleri benzerleriyle gruplama sürecine kümeleme denir. Kümeleme analizi, temel amacı nesneleri (birim) sahip oldukları karakteristik özellikleri baz alarak gruplamak olan çok değişkenli teknikler grubudur. Eldeki veriler yardımıyla analiz yaparken, verimli ve güvenilir analiz yapma açısından kümeleme analizi oldukça büyük bir önem taşımaktadır. Örneğin, Türkiye’deki şehirlerin profilini çıkarmak üzere bir araştırma yapılacaktır. Tarıma dayalı bir gelir sistemi olan bir şehri, geliri sanayiye dayalı olan şehirlerle kıyaslamak ne kadar güvenilir sonuçlar verir tartışılır. Aynı şekilde nüfusu milyonlarla ölçülen şehirleri nüfusu yüz binler olan şehirlerle kıyaslamak da yanlıştır. Belirlenen kriterlere göre benzer özellik gösteren şehirler bir gruba toplanır ve kendi aralarında analiz yapılır.
 |
| Şehirleri kümeleme yöntemi örneği |
Örneğin, Hakkari’yi Ankara ile kıyaslamak yerine profili benzer olabilecek Siirt, Batman, Muş vb. şehirlerle kıyaslamak çok daha güvenilir sonuçlar elde edilmesini sağlayacaktır [6].
Kümeler oluşturulurken, kümenin içinde yer alan nesneler arası benzerlik en büyük, kümeler arası benzerlik ise en küçük olacak şekilde olmalıdır. Benzer bir ifade ile kümeleme analizinin amacı, var olan verileri içsel olarak homojen, kümeler arası heterojen olarak ayırmaktır. Kümeleme analizi genellikle market araştırmaları, gen araştırmaları gibi konularda sıklıkla kullanılır. Bu veriler arasında nitelik bakımından ilginç korelasyonlar elde edilebilir. Örneğin, tıp alanında benzer özelliklere sahip genler aynı küme içine alınabilir.
Kümeleme modellerinde amaç üyelerinin birbirlerine çok benzediği, ancak özellikleri birbirlerinden çok farklı olan kümelerin bulunması ve veri tabanındaki kayıtların bu farklı kümelere bölünmesidir. Veri tabanındaki kayıtların hangi kümelere ayrılacağı veya kümelemenin hangi değişken özelliklerine göre yapılacağı konunun uzmanı olan bir kişi tarafından belirtilebileceği gibi veri tabanındaki kayıtların hangi kümelere ayrılacağını geliştirilen bilgisayar programları da yapabilmektedir.
Marketlerde farklı müşteri gruplarının keşfedilmesi ve bu grupların alışveriş örüntülerinin ortaya konması, biyolojide bitki ve hayvan sınıflandırmaları ve işlevlerine göre benzer genlerin sınıflandırılması, şehir planlanmasında evlerin tiplerine, değerlerine ve coğrafik konumlarına göre gruplara ayrılması gibi uygulamalar tipik kümeleme uygulamalarıdır. Kümeleme aynı zamanda Web üzerinde bilgi keşfi için dokümanların sınıflanması amacıyla da kullanılabilir [17].
Veri kümeleme güçlü bir gelişme göstermektedir. Veri tabanlarında toplanan veri miktarının artmasıyla orantılı olarak, kümeleme analizi son zamanlarda veri madenciliği araştırmalarında aktif bir konu haline gelmiştir. Literatürde pek çok kümeleme algoritması bulunmaktadır. Kullanılacak olan kümeleme algoritmasının seçimi, veri tipine ve amaca bağlıdır.
Genel olarak başlıca kümeleme yöntemleri şu şekilde sınıflandırılabilir [1]:
- Bölme yöntemleri (Partitioning methods),
- Hiyerarşik yöntemler (Hierarchical methods),
- Yoğunluk tabanlı yöntemler (Density-based methods),
- Izgara tabanlı yöntemler (Grid-based methods),
- Model tabanlı yöntemler (Model-based methods).
Bölme yöntemlerinde, n veri tabanındaki nesne sayısı ve k oluşturulacak küme sayısı olarak kabul edilir. Bölme algoritması n adet nesneyi, k adet kümeye böler (k n) . Kümeler tarafsız bölme kriteri olarak nitelendirilen bir kritere uygun oluşturulduğu için aynı kümedeki nesneler birbirlerine benzerken, farklı kümedeki nesnelerden farklıdırlar. Bölme yöntemlerinde içerisinde kullanılan en yaygın yöntem ise k-means yöntemidir [1].
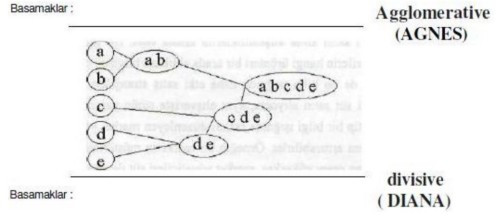
Hiyerarşik yöntemler, veri nesnelerini kümeler ağacı şeklinde gruplara ayırma esasına dayanır. Hiyerarşik kümeleme yöntemleri, hiyerarşik ayrışmanın aşağıdan yukarıya veya yukarıdan aşağıya doğru olmasına göre agglomerative ve divisive hiyerarşik kümeleme olarak sınıflandırılabilir [18].
Agglomerative hiyerarşik kümelemede, şekilde görüldüğü gibi hiyerarşik ayrışma aşağıdan yukarıya doğru olur. İlk olarak her nesne kendi kümesini oluşturur ve ardından bu atomik kümeler birleşerek, tüm nesneler bir kümede toplanıncaya dek daha büyük kümeler oluştururlar. Divise hiyerarşik kümelemede, şekilde görüldüğü üzere hiyerarşik ayrışma yukarıdan aşağıya doğru olur. İlk olarak tüm nesneler bir kümededir ve her nesne tek başına bir küme oluşturana dek, kümeler daha küçük parçalara bölünürler [18].
Birliktelik kuralları
Birliktelik kuralları, büyük veri kümeleri arasında birliktelik ilişkileri bulurlar. Toplanan ve depolanan verinin her geçen gün artması yüzünden, şirketler veri tabanlarındaki birliktelik kurallarını ortaya çıkarmak istemektedirler. Büyük miktardaki mesleki işlem kayıtlarından ilginç birliktelik ilişkilerini keşfetmek, şirketlerin karar alma işlemlerini daha verimli hale getirmektedir.
Birliktelik kurallarının kullanıldığı en tipik örnek market sepeti uygulamasıdır. Bu işlem, müşterilerin yaptıkları alışverişlerdeki ürünler arasındaki birliktelikleri bularak müşterilerin satın alma alışkanlıklarını analiz eder. Bu tip birlikteliklerin keşfedilmesi, müşterilerin hangi ürünleri bir arada aldıkları bilgisini ortaya çıkarır ve market yöneticileri de bu bilgi ışığında daha etkili satış stratejileri geliştirebilirler.
Örneğin, bir müşteri süt satın alıyorsa, aynı alışverişte sütün yanında ekmek alma olasılığı nedir? Bu tip bir bilgi ışığında rafları düzenleyen market yöneticileri ürünlerindeki satış oranını arttırabilirler. Örneğin, bir marketin müşterilerinin süt ile birlikte ekmek satın alan oranı yüksekse, market yöneticileri süt ile ekmek raflarını yan yana koyarak ekmek satışlarını arttırabilirler.
Birliktelik kuralının matematiksel modeli Agrawal, Imielinski ve Swami tarafından 1993 yılında sunulmuştur [19]. Bu modelde, I ={i1,i2,..,im} kümesine “ürünler” adı verilmektedir. D, veri bütünlüğündeki tüm hareketleri, T ise ürünlerin her bir hareketini simgeler. TID ise, her harekete ait olan tek belirteçtir [20].
Birliktelik kurallarına ait örnekler şöyle olabilir:
- “Müşteriler bira satın aldıklarında %75 olasılıkla çocuk bezi de satın alırlar.”
- “Düşük yağlı peynir ve yağsız süt alan müşteriler %85 olasılıkla diyet süt alırlar.”
Ardışık analiz ise birbiriyle ilişkisi olan ancak birbirini izleyen dönemlerde gerçekleşen ilişkilerin tanımlanmasında kullanılır. Ardışık analize ait örnekleri şöyle olabilir.
- “Çadır alan müşterilerin %10'u bir ay içerisinde sırt çantası almaktadır.”
- “A hissesi %15 artarsa üç gün içinde B hissesi %60 olasılıkla artacaktır.”
Birliktelik kuralına ilişkin olarak geliştirilen bazı algoritmalar şunlardır; AIS, SETM, Apriori, Partition, RARM, CHARM.
Bu algoritmalar içerisinde, ilk olanı AIS, en bilineni ise Apriori algoritmasıdır [20].
KAYNAKLAR
[1] İnternet: Hacettepe Üniversitesi “Veri Madenciliğine Giriş” http://yunus.hacettepe.edu.tr/~hcingi/ist376a/6Bolum.doc (2011)
[2] Giudici, P., “Applied Data Mining: Statistical Methods for Business and Industry”, John Wiley & Sons Inc., Chichester, 85–100 (2003).
[3] Akbulut, S., “Veri madenciliği teknikleri ile bir kozmetik markanın ayrılan müşteri analizi ve müşteri segmentasyonu”, Yüksek Lisans Tezi, Gazi Üniversitesi Fen Bilimleri Enstitüsü, Ankara, 1–25 (2006).
[4] Koyuncugil, A.S. ve Özgülbaş, N., “Veri madenciliği: tıp ve sağlık hizmetlerinde kullanımı ve uygulamaları”, Bilişim Teknolojileri Dergisi, 2(2): 21–32 (2009).
[5] Ayık, Y.Z., Özdemir, A. ve Yavuz, U., “Lise türü ve lise mezuniyet başarısının kazanılan fakülte ile ilişkisinin veri madenciliği tekniği ile analizi”, Sosyal Bilimler Enstitüsü Dergisi, 10(2): 441–454 (2007).
[6] Albayrak, M., “EEG sinyallerindeki epileptiform aktivitenin veri madenciliği süreci ile tespiti”, Doktora Tezi, Sakarya Üniversitesi Fen Bilimleri Enstitüsü, Sakarya, 56–70 (2008).
[7] Uğur, A. ve Kınacı, A.C., “Yapay zeka teknikleri ve yapay sinir ağları kullanılarak web sayfalarının sınıflandırılması”, Inet-tr 2006, XI. Türkiye’de İnternet Konferansı, TOBB Ekonomi ve Teknoloji Üniversitesi, Ankara, (2006).
[8] Savaş, S., Topaloğlu, N., Kazcı, Ö. et al. Classification of Carotid Artery Intima Media Thickness Ultrasound Images with Deep Learning. J Med Syst 43, 273 (2019). https://doi.org/10.1007/s10916-019-1406-2
[9] Shah. S. ve Kursak. A., “Data mining and genetic algorithms based gene / SNP selection”, Artificial Intelligence in Medicine, 31, 183 -196 (2004).
[10] Çiftci, S., “Uzaktan eğitimde öğrencilerin ders çalışma etkinliklerinin log verilerinin analiz edilerek incelenmesi”, Yüksek Lisans Tezi, Gazi Üniversitesi Eğitim Bilimleri Enstitüsü, Ankara, 1–5 (2006).
[11] Han, J. ve Kamber, M., “Data Mining: Concepts and Techniques”, Morgan Kaufmann, San Francisco, USA, 45–53 (2001).
[12] Larose, D.T., “Discovering Knowledge in Data: An Introduction to Data Mining”, John Wiley & Sons Inc., 42–70 (2005).
[13] Shah. S. ve Kursak. A., “Data mining and genetic algorithms based gene / SNP selection”, Artificial Intelligence in Medicine, 31, 183 -196 (2004).
[14] Çalışkan, S.K. ve Soğukpınar, İ.,”KxKNN: K-Means ve k en yakın komşu yöntemleri ile ağlarda nüfuz tespiti”, 2. Ağ ve Bilgi Güvenliği Sempozyumu, Girne, 120–124 (2008).
[15] Hui, S. ve Jha, G., “Application data mining for customer service support”, Information and Management, 38: 1–13 (2000).
[16] Pawlak, Z., “Rough sets, decision algorithms and bayes theorem”, Europen Journal of Operation Research, 136: 181–189 (2002).
[17] Seidman, C., “Data Mining With Microsoft SQL Server 2000”, Microsoft Press, Washington, USA, (2001).
[18] Özekes, S., “Veri madenciliği modelleri ve uygulama alanları”, İstanbul Ticaret Üniversitesi Dergisi, 3: 65–82 (2003).
[19] Agrawal, R., Imielinski, T. ve Swami, A., “Mining association rules between sets of ıtems in large databases”, In Proceedings of the ACM SIGMOD International Conference on Management of Data (ACMSIGMOD ’93), Washington, USA, 207–216 (1993).
[20] Özçakır, F.C. ve Çamurcu, A. Y., “Birliktelik kuralı yöntemi için bir veri madenciliği yöntemi tasarımı ve uygulaması”, İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi, 6(12): 21–37 (2007).