Derin öğrenme mimarileri oluşturulurken, kullanılacak algoritma büyük önem taşımaktadır. Bu algoritmalar verinin türüne, boyutuna, hacmine ve yapısına, kullanılacak olan parametrelere göre farklılık gösterebilmektedir. Evrişimsel Sinir Ağları (ESAConvolutional Neural Network — CNN), Tekrarlayan Sinir Ağı (Recurrent Neural Network-RNN), Kısıtlı Boltzmann Makineleri (Restricted Boltzmann Machines-RBM) ve Derin İnanç Ağları (Deep Belief Nets-DBN) bunlardan başlıcalarıdır.
Evrişimsel sinir ağları
Derin öğrenme algoritmalarının içinde en bilineni CNN’dir. Görüntü sınıflandırma problemlerinde sıklıkla kullanılmaktadır. CNN’de her bir katmanda matris üzerinde işlem yapan genellikle boyutları 3x3, 5x5, 7x7 olan filtreler (çekirdekler) kullanılmaktadır. Daha sonra bu filtrelerin çıktılarının üzerinde havuzlama (pooling) işlemi yapılmaktadır. Havuzlama ile çekirdekte bulunan veriler filtrelenir. Max pooling yöntemi sıklıkla kullanılan havuzlama yöntemi olup bu yöntemde matris içindekilerden en büyüğü alınır.
 |
| Evrişimsel katman (3x3) |
 | ||
| Havuzlama (2x2) |
CNN’de, bazı filtreler çok katmanlı bir sinir ağındaki w parametresi gibi öğrenme parametreleri olarak işlev görür. Genelde evrişim işlemlerinde kullanılırlar. Evrişim sırasında seçilen filtre, her seferinde görüntü üzerinde kaydırılır. İşlem sırasında filtrenin değerleri, o pencere boyutundaki görüntünün değerleri ile çarpılır. Sonucunda ise görüntünün tüm değerlerini bu pencere boyutunda temsil eden tek bir sayı oluşur.
CNN’de işlem yapılan görüntü matris formatındadır. Şekil’de 6x8 boyutunda bir görüntü matrisi ve 3x3 boyutunda bir çekirdek matrisi görülmektedir. Görüntü matrisine uygulanan filtre sayesinde görüntü üzerinden belli özellikler üzerinde karşılaştırma yapılarak görüntüden veriler elde edilmektedir. Algoritmayı kullanırken seçilen kütüphaneler, çekirdek filtrelerini otomatik olarak seçebilmektedir. Parametrelerin doğru olarak tanımlanması da önemlidir. Bu işlem ile görüntü üzerinde bazı özellikler yakalanmaya çalışılır. Bu sayede belli bir olasılıkla resmin görüntünün hangi sınıfa ait olduğu tespit edilir. Bu işlemler diğer görüntüler üzerinde de uygulanarak, benzerlikler kurulmaya çalışılır. Belirlenen filtre görüntü üzerinden kaydırılarak resmin tamamına uygulanır. Bu kaydırma işlemi “stride” denilen adım sayısına göre gerçekleştirilir [1].
Havuzlama katmanında ise öğrenilen parametre yoktur. Burada girdi olarak verilen matrisin kanal sayısını sabit kalır ancak yükseklik ve genişlik bilgisi indirgenir. Bu adımda hesaplama karmaşıklığı azaltılır. Şekil’de 4x6 boyutundaki matrise, 2x2 boyutunda maksimum ve ortalama havuzlama işlemleri uygulanmış, bunun sonucunda her bir 4 elemanın 1 çıkışı olmuştur. Böylece matris dörtte üç oranında küçültülmüş olur.
İki fonksiyonun (𝑓 & 𝑔) sonlu aralıktaki [0, 𝑡] evrişimi [2]:
Burada [𝑓 ∗ 𝑔](𝑡), 𝑓 ve 𝑔 fonksiyonlarının evrişimi anlamına gelmektedir. Evrişim daha çok sonsuz bir aralıkta alınır [2]:
Bir CNN modelinin iki önemli avantajı vardır. Bunlardan ilki, önemli ölçüde öğrenilmesi gereken filtrelerin parametrelerine indirgemedir. Çok fazla nöronun öğrenilmesi ve ihtiyaç duyulması için birçok parametre olduğunda, birçok sorun ortaya çıkmaya başlayabilir. Giriş olarak yüksek çözünürlüğe sahip bir görüntü varsa, piksellere göre bir milyon değere sebep olur. Aşırı öğrenmeye sebep olabilecek ve çok fazla hesaplama gücü gerektiren çok derin ve tam olarak bağlı katmanlara ihtiyaç duyacaktır. Bununla birlikte CNN, özellikle bilgisayarla görme işlemlerde, aşırı öğrenme olasılığını azaltabilir ve hesaplama gücünü koruyabilir [3].
İkinci ana avantaj parametre paylaşımıdır. CNN ile öğrenilen parametreler bir sonraki katmana girdi olarak paylaşılır. Bu sebeple, aynı ağırlıklar katmandan tekrar kullanılır, bu da katmanlarda tekrar öğrenmeye gerek olmadığı anlamına gelir. Bu şekilde, daha sonraki katmanlar daha karmaşık özellik ve kalıpları öğrenebilir [3].
Veriyi işleyerek öğrenen modelleri tasarlarken, tasarımcılar kullanılacak algoritmaya ve tekniklere de karar vermektedir. Bu karar beraberinde bazı parametreleri de getirir. K en yakın komşu (K Nearest Neighbor-KNN) algoritmasındaki “k” değeri, SVM algoritmasında kullanılacak çekirdek fonksiyonu ve derin öğrenme modellerinde seçilen “seyreltme (Drop Out)” değerleri gibi bazı parametreler, modeli tasarlayan tarafından belirlenir. Bu belirleme işlemi verinin türüne, ele alınan konuya ve verinin boyutuna bağlı olarak değişebilmektedir.
Bu açıklamalardan yola çıkarak, hiper-parametre kavramı ortaya atılmıştır. Ne olması gerektiği, modeli tasarlayan kişiye bırakılmış, probleme, veri setine göre değişiklik gösteren parametreler hiper-parametre (hyperparameters) olarak adlandırılmaktadır [4].
Oluşturulacak modelde kullanılacak hiper-parametreler, derin öğrenme uygulamalarındaki en önemli problemlerden birisidir. Hiper-parametreler ve bunların değerlerinin seçimi, verinin türüne, programcının tecrübesine ve sezgisine, yeni çalışmalara, farklı uygulamalarda elde edilen sonuçlar vb. gibi pek çok duruma bağlı olarak değişmektedir. Model tasarlanırken kullanılabilecek parametrelerden başlıcaları şunlardır:
- Ağda Kullanılacak Çekirdek Boyutu
- Parti büyüklüğü sayısı (Batch-size)
- Çevrim Sayısı
- Katman Sayısı
- Kullanılacak Aktivasyon Fonksiyonu
- Optimizasyon Algoritması
- Öğrenme Hızı (Learning Rate)
- Seyreltme (Drop Out) Değeri
- Seyreltme Kullanılacak Yerler
- Veri Setinin Büyüklüğü
Pek çok çalışmada bu hiper-parametreler, test et/sonucu yorumla yöntemiyle defalarca tekrarlanan çalışmalar sonucunda belirlenir. Modele en uygun olanı ve en iyi sonuç vereni, programcı tarafından belirlenerek, modelin son hali kaydedilir.
Tekrarlayan sinir ağı (RNN)
Tipik sinir ağlarında genel olarak, her girdi ve çıktının diğerlerinden bağımsız olduğu varsayılır ancak bu varsayım bazı problemlerde doğru sonuç vermemektedir. Sıralı girdilerin kullanıldığı problemlerde (cümle-kelime ilişkisi gibi)önceki girdi bilgilerine ihtiyaç duyulmaktadır. Tekrarlayan sinir ağları, girdiler dizisindeki tüm elemanların hesaplamasını ayrı ayrı yapar ve her çıktı elemanı da mevcut girdiye ek olarak önceki hesaplamalara bağlıdır. Şekil’de basit bir RNN yapısı gösterilmiştir [5]. Ayrıca geleneksel bir RNN mimarisinin artıları ve eksileri Çizelge’de verilmiştir [6].
 |
| Basit bir RNN yapısı |
 |
| RNN mimarisinin avantaj ve dezavantajları |
Uzun Kısa Süreli Bellek ağları, RNN’lerin uzun süreli hatırlama problemlerini çözmek amacıyla ortaya çıkmıştır.
Kısıtlı Boltzmann makineleri
Boltzmann makinelerinin görünür ve gizli katmanda yer alan birimlerin katman içindeki bağlantılarının kaldırıldığı basitleştirilmiş yapılardır. En büyük avantajı katmanlara ait birimler diğer katmanın bilinmesi durumunda şartlı olarak bağımsızdır. Görünür veya gizli birimler dışarıda bırakıldığında diğer katmana ait birimlerin genel olarak çarpanlarına ayrılması mümkündür. Görünür katmanın tüm birimlerinin alabileceği olası tüm değerler üzerinden integrali tek boyutlu integral şeklinde hesaplanabilir. Bu durum tahmin çıkarımında örneklem yönteminin doğru sonuçlar üretmesine imkân sağlar [7].
Gizli birimler ve giriş birimleri arasındaki bağlantı yönlendirilmez. Boltzmann makinelerinde uygulanan verimsiz örnekleme gibi pratik sınırlamalarını önlemek için, yapısal olarak Boltzmann makinelerinin sınırlandırılmış bir versiyonu olarak önerilmiştir [7].
 |
| Kısıtlı Boltzmann makineleri diyagramı |
Kısıtlı Boltzmann makinelerinde öğrenme oranlarının seçiminde titiz teorik bir arka plan çalışması olmamasından dolayı genellikle her iki eşik değerini (bias) öğrenmek için nispeten daha küçük öğrenme oranları kullanılır. Kısıtlı Boltzmann makineleri, Boltzmann makinelerinden türetilmiş özel bir yapı olduğundan öğrenme işlemi için Boltzmann makinelerinde kullanılan Gibbs örneklemesinin kullanılması mümkündür. Kısıtlı yapısı sayesinde Gibbs örneklemesi daha verimli olarak kullanılabilir, verilen katman ister görünür ister gizli katman olsun, diğer katmanlardaki birimlerden karşılıklı olarak bağımsız hale gelir. Kısıtlı Boltzmann makineleri, nöronların sayısı arttıkça, temsil edilen olasılık dağılımının daha derli toplu açıklanması için Gibbs örnekleme yöntemi tarafından daha fazla sayıda örnek toplanmak zorundadır. Ayrıca, Gibbs örnekleme yöntemi yapısı gereği, örnekler dağıtımın bazı kısımlarını gözden kaçırabilirler [8].
Derin inanç ağları
Derin inanç ağları, giriş katmanı olan bir görünür katmandan ve birden çok gizli katmandan oluşur. Birden fazla kısıtlı Boltzmann makineleri katmanı istiflenerek oluşturulur. Derin inanç ağlarının üst iki katı bir kısıtlı Boltzmann oluşturur ve alt katmanlar yönlendirilmiş bir sigmoid inanç ağı oluşturur [9].
Derin inanç ağları çoklu stokastik, gizli değişken katmanlarından oluşan olasılıksal üretici modellerdir. Gizli değişkenler tipik olarak ikili değerlere sahiptir ve genellikle gizli birimler veya özellik dedektörleri olarak adlandırılır. Üstteki iki katman, aralarında yönlendirilmemiş, simetrik bağlantılara sahiptir ve ilişkili bir hafıza oluşturur. Alt katmanlar, yukarıdaki katmandan yukarıdan aşağıya doğru yönlendirilmiş bağlantılar alır. En alt katmandaki birimlerin durumları bir veri vektörünü temsil eder. Derin inanç ağlarının en önemli iki özelliği [10]:
- Bir katmandaki değişkenlerin, yukarıdaki katmandaki değişkenlere nasıl bağlı olduğunu belirleyen, üretici ağırlıkları öğrenmek için yukarıdan aşağıya etkili bir katman-katman prosedürü vardır.
- Öğrenmeden sonra, her katmandaki gizli değişkenlerin değerleri, alt katmandaki gözlenen bir veri vektörüyle başlayan ve ters yönde üretici ağırlıkları kullanan tek, aşağıdan yukarıya bir geçişle çıkarılabilir.
Derin inanç ağları, bir kerede gizli değişkenlerin değerlerini işleyerek bir sonraki katmanı eğitmek için veriler olarak verilerden çıkarıldıkları zaman, bir seferde bir katman öğrenir. Bu verimli, açgözlü öğrenmeyi, tüm ağın üretici veya ayırt edici performansını iyileştirmek için tüm ağırlıklara ince ayar yapan diğer öğrenme prosedürleri izleyebilir veya bunlarla birleştirilebilir. İstenen çıktıları temsil eden son bir değişkenler katmanı ve geri yayılma hata türevleri eklenerek, ayırt edici ince ayar yapılabilir [10].
Dünden Bugüne Yapay ZekaKAYNAKLAR
[1] Okumuş, R. (2019). Convolutional Neural Networks (Evrişimsel Sinir Ağları). Web: https://medium.com/@rabiaokumus96/convolutional-neuralnetworks-evri%C5%9Fimsel-sinir-a%C4%9Flar%C4%B1-cceb887a2979
[2] Weisstein, E. W. (2019). Convolution. Web: http://mathworld.wolfram.com/Convolution.html
[3] Satar, B. (2018). Deep Learning Based Vehicle Make And Model Classification, Yüksek Lisans Tezi, Uludağ Üniversitesi Fen Bilimleri Enstitüsü, Bursa.
[4] Çarkacı, N. (2018). Derin Öğrenme Uygulamalarında En Sık kullanılan Hiperparametreler. Web: https://medium.com/deep-learning-turkiye/derin-ogrenmeuygulamalarinda-en-sik-kullanilan-hiper-parametreler-ece8e9125c4
[5] Günel, K., İşman, G., ve Kocakula, M. (2018). Simple recurrent neural networks for the numerical solutions of ODEs with Dirichlet boundary conditions. BAUN Fen Bil. Enst. Dergisi, 143–153. doi: 10.25092/baunfbed.483922
[6] Amidi, A., and Amidi, S. Tekrarlayan Yapay Sinir Ağları el kitabı. Web:
https://stanford.edu/~shervine/l/tr/teaching/cs-230/cheatsheet-recurrent-neuralnetworks
[7] Özcan, H. (2014). Çok Düşük Çözünürlüklü Yüz İmgelerinde Derin Öğrenme Uygulamaları. İstanbul: T.C. Deniz Harp Okulu Deniz Bilimleri ve Mühendisliği Enstitüsü.
[8] Tiken, C. (2015). Derin Öğrenme Uygulamaları, Yüksek Lisans Tezi, İstanbul Üniversitesi Fen Bilimleri Enstitüsü, İstanbul.
[9] Elitez, O. (2015). Handwritten Digit String Segmentation And Recognition Using Deep Learning. Yüksek Lisans Tezi, Middle East Technical University, Ankara.
[10]Hinton, G. E. (2009). Deep belief networks. doi:10.4249/scholarpedia.5947
[11] Savaş, S. (2019), Karotis Arter Intima Media Kalınlığının Derin Öğrenme ile Sınıflandırılması, Gazi Üniversitesi Fen Bilimleri Enstitüsü Bilgisayar Mühendisliği Ana Bilim Dalı, Doktora Tezi, Ankara.

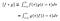


Hiç yorum yok:
Yorum Gönder